|
|---|
| Útima modificação : 14 de julho de 1995. | This Page in English (comming soon) |
A solução de sistemas lineares por decomposição LU tem grande importância nos processos computacionais técnicos e científicos, principalmente na área de computação gráfica.
Para compreender a decomposição LU, é preciso antes conhecer os algoritmos de resolução de sistemas lineares pelo método da eliminação de Gauss, os quais estão intimamente ligados à decomposição LU.
Este trabalho foi baseado no artigo de J. M. Ortega [3] o qual faz a análise das várias formas da eliminação de Gauss baseada na forma genérica de três laços dada na figura 1.
|
|---|
O método de eliminação de Gauss consiste no seguinte:
Seja o sistema linear A.x = b onde A é uma matriz mxm, triangular superior com elementos da diagonal principal diferentes de zero. O sistema fica, então, da seguinte maneira:
|
|---|
Da última equação, temos
|
|---|
x[n-1] pode, então, ser obtido da penúltima equação:
|
|---|
A partir disso, é possível descrever um algoritmo para a solução deste tipo de sistema linear.
Dado um sistema triangular superior nxn com elementos da diagonal principal da matriz A não nulos. Então teremos:
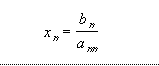
|
|---|
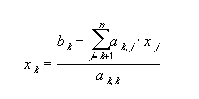
|
|---|
Com isso, o método da eliminação de Gauss consiste em transformar um sistema de equações lineares cuja matriz de coeficientes não é triangular superior num sistema equivalente - se existir - cuja matriz de coeficientes seja triangular superior. Para obter a matriz triangular superior, basta aplicar o seguinte algoritmo:
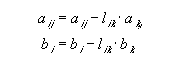
|
|---|
onde
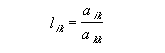
|
|---|
Desta forma, podemos obter as matrizes L e U pelo método da eliminação de Gauss, onde:
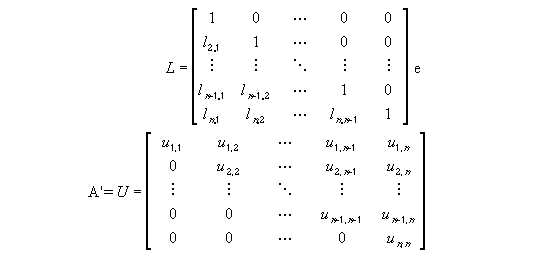
|
|---|
sendo A' a matriz dos coeficientes resultante da aplicação do método da eliminação de Gauss.
Desta forma, temos a forma canônica do algoritmo do método da eliminação de Gauss:
|
|---|
A versão IJK calcula os elementos da matriz L por linha, sendo que para cada elemento L[i][j-1],
é feito o cálculo do elemento A[i][j], subtraindo deste elemento os elementos da primeira
linha até o elemento da linha j-2 da matriz A, multiplicados pelos elementos da linha i, da
primeira coluna até o elemento da coluna j-2 da matriz L (A[i][j] = A[i][j] - L[i][k] *
A[k][j]).
|
|---|
|
|---|
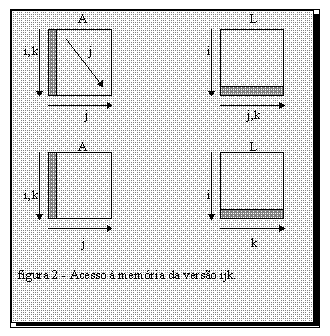
O acesso da matriz A é feito por colunas e o da matriz L por linhas (região cinza-escuro).
Como na linguagem C as matrizes são armazenadas na memória por linhas, o acesso por colunas
à matriz A pode ser considerada ruim já que não permite o aproveitamento do cache.
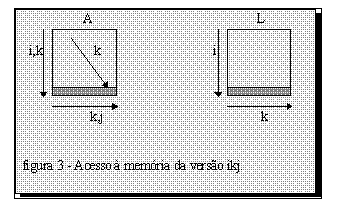
Esta é a versão mais simples da decomposição LU. Nesta versão, para cada elemento L[i][k] calculado calcula-se os elementos da linha i e colunas de k+1 até n-1 da matriz A. Para cada elemento A[i][j] é subtraído o elemento da linha k, coluna j de A multiplicado pelo elemento da linha i, coluna k de L (A[i][j] = A[i][j] - L[i][k] * A[k][j]).
|
|---|
|
|---|
Neste caso, tanto a matriz A quanto a matriz L são acessadas por linha, sendo então um
dos melhores algoritmos.
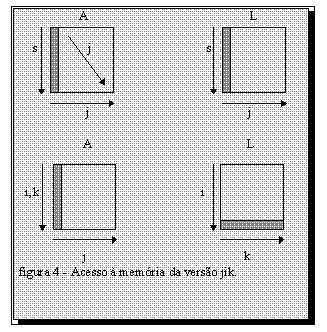
Nesta versão, para cada coluna j-1, são calculados os valores de L a partir da linha j até a linha n-1. Em seguida é feito o cálculo com os elementos da matriz A a partir da linha 1 até a linha j, calculando para cada linha i o elemento A[i][j], subtraindo deste elemento os elementos da coluna j, linhas de 0 até i-1 da matriz A multiplicados, respectivamente, pelos elementos da linha i, colunas de 0 até i-1 da matriz L (A[i][j] = A[i][j] - L[i][k] * A[k][j]). Por último, para cada elemento da matriz A a partir da linha j+1 até a linha n-1, são calculados os elementos A[i][j], subtraindo destes elementos os elementos da coluna j, linhas de 0 até j-1 da matriz A multiplicados pelos elementos da linha i, colunas de 0 até j-1 da matriz L (A[i][j] = A[i][j] - L[i][k] * A[k][j]).
|
|---|
|
|---|
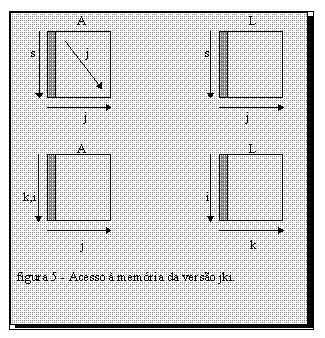
Nesta versão, para cada coluna j-1, são calculados os valores de L a partir da linha j até a linha n-1. Em seguida é feito o cálculo com os elementos da matriz A a partir da linha 1 até a linha j, calculando para cada linha i o elemento A[i][j], subtraindo deste elemento os elementos da coluna j, linhas de 0 até j-1 da matriz A multiplicados, respectivamente, pelos elementos da linha i, colunas de 0 até j-1 da matriz L (A[i][j] = A[i][j] - L[i][k] * A[k][j]).
|
|---|
|
|---|
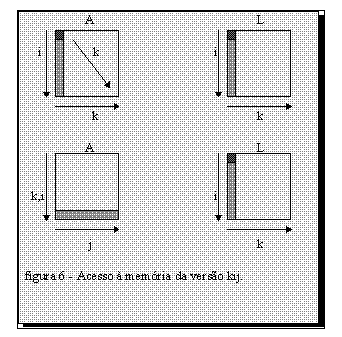
Nesta versão, para cada elemento L[i][k] calculado, são calculados os elementos da linha i, colunas de k+1 até n-1 da matriz A, subtraindo-se, respectivamente, os elementos da linha k, colunas de k+1 até n-1 da matriz A multiplicados pelo elemento L[i][k] (A[i][j] = A[i][j] - L[i][k] * A[k][j]).
|
|---|
|
|---|
Nesta última versão, para cada coluna k, são calculados os elementos da matriz L a partir da linha k+1 até n-1 e, em seguida, são calculados os elementos A[i][j] com i e j variando de k+1 até n-1 (A[i][j] = A[i][j] - L[i][k] * A[k][j]).
|
|---|

|
|---|
Aqui tanto a matriz A quanto a matriz L são exclusivamente acessadas por colunas sendo,
portanto, considerado ruim, pois, não garante o reuso do cache.
|
|---|
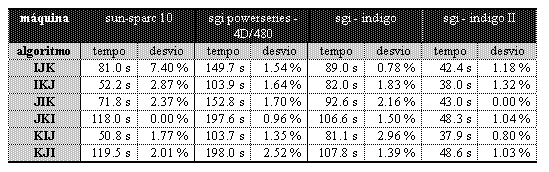
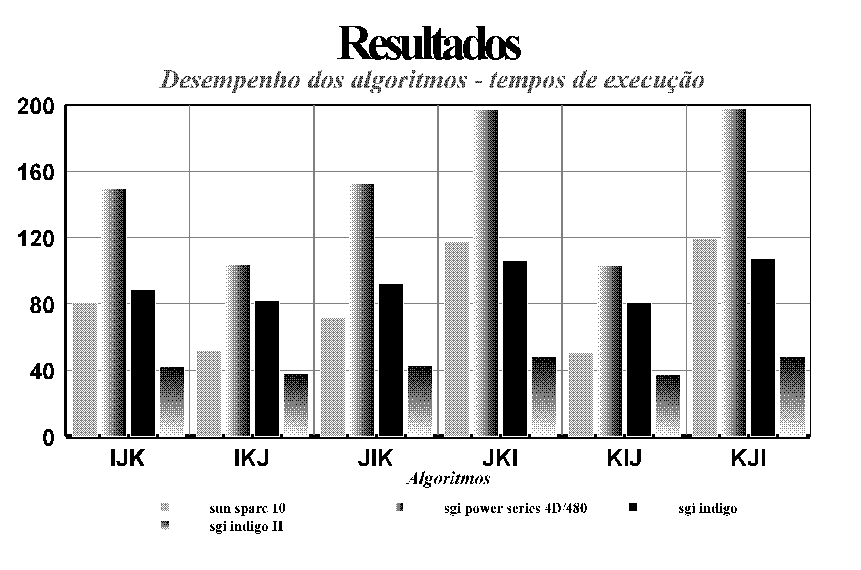
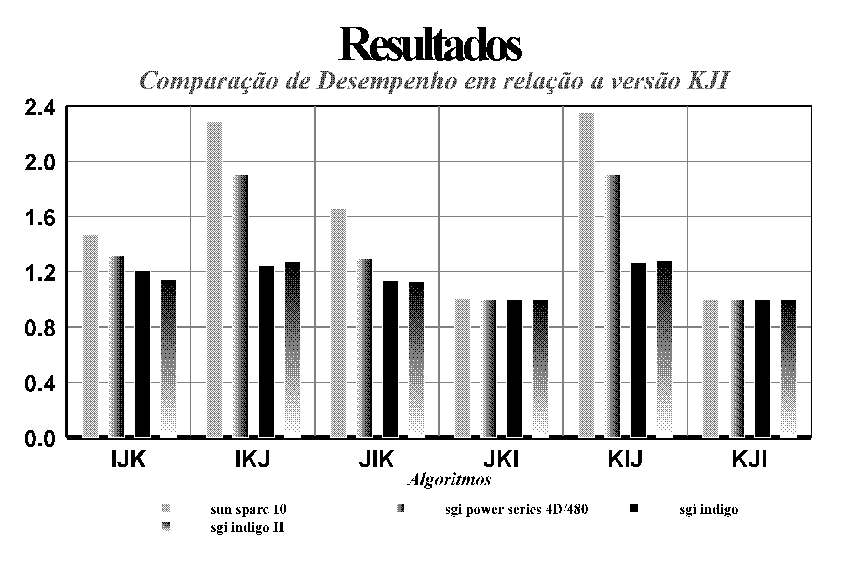
Verificamos por esta tabela que o algoritmo com o pior desempenho, em todas as máquinas foi a
versão KJI e que a melhor foi a versão KIJ. As medidas foram realizadas usando o comando
Para as medidas na SGI Power Series, foi utilizado o comando runon o qual especifica em qual
processador (dos oito existentes) o programa será executado. Isto é necessário
para que não ocorra a troca entre os processadores o que causaria perda das informações
no cache.
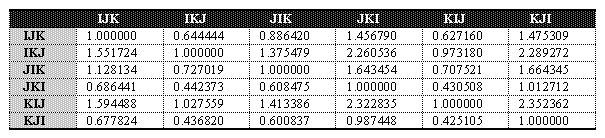
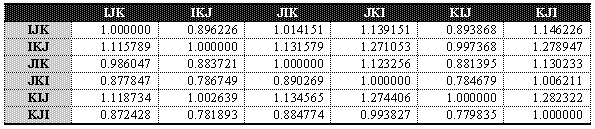
Abaixo, tabelas de comparação de desempenho relativo entre os diversos algoritmos para as
três máquinas.
Estas tabelas foram obtidas fazendo-se a razão dos tempos de execução dos algoritmos
de cada coluna com os tempos de execução dos algoritmos das linhas. Assim, quanto menor o
tempo de execução do algoritmo, melhor o seu desempenho.
time( ) da linguagem C, calculando-se apenas o
tempo transcorrido para a execução dos loops da decomposição LU, desconsiderando-se as
inicializações. Os programas foram compilados com o compilador gcc sem diretivas de
otimização. As matrizes usadas foram de dimensões 512 x 512 do tipo float.
|
|---|
|
|---|
|
|---|
|
|---|